
Capítulo 4: Líneas especiales en triángulos, cuadriláteros, perpendiculares y desigualdades
Lineas especiales de un triángulo
Altura
La altura es un segmento perpendicular trazado desde el vértice hasta al lado opuesto del triángulo
Todo triángulo tiene 3 alturas
La intersección de 3 alturas se llama ortocentro
Figura interactiva 26
Mediana
Bisectriz
Mediatriz
La mediana es un segmento que une el punto medio de un segmento con el vértice opuesto
Todo triángulo tiene 3 medianas
La intersección de 3 medianas se llama baricentro
Es un segmento bisectriz de un determinado ángulo del triángulo
Todo triángulo tiene 3 bisectrices
La intersección de 3 bisectrices se llama incentro
El es segmento perpendicular al punto medio de un segmento del triángulo
Todo triángulo tiene 3 mediatrices
La intersección de 3 mediatrices se llama circuncentro
Ejercicios


Práctica realizando los ejercicios y pregunta si tienes alguna duda
Cuadriláteros
Sean A,B,C y D, cuatro puntos coplanarios, si 3 cualesquiera de ellos no están alineados, los segmentos AB, BC, CD, y AD forman un cuadrilátero.
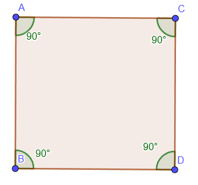
Cuadrado
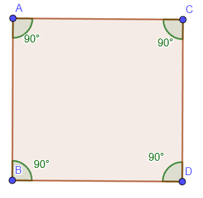
Rectángulo
Si los 4 lados de un cuadrilátero son congruentes y los 4 ángulos son rectos, entonces el cuadrilátero se llama cuadrado
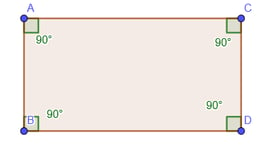
Si los 4 ángulos de un cuadrilátero son rectos, entonces el cuadrilátero se llama rectángulo

Ejercicios
Practica realizando los ejercicios de: la página 145 - 4; la página 146 - 6,9,12,13 ; la página 148 - 9,13,14,15,16,17 y la página 149 - 18,19,20,21,22,23,24,25
Perpendiculares
Teorema 29
Teorema 30
Teorema 31
Teorema 32
Teorema 33 - Teorema de la mediatriz
Teorema 34 - Teorema LAA
Teorema 35 - Teorema H-C (Hipotenusa- Cateto)
En un plano dado, y por un punto dado de la recta dada, pasa una, y solamente una recta perpendicular a la recta dada
En un plano dado, desde un punto externo dado a una recta l, hay una unica recta perpendicular a la recta l.
Si M está entre los puntos A y C de una recta l, entonces M y A están al mismo lado que otra recta que contenga a C.
Si M está entre los puntos B y C, y A es un punto cualquiera fuera de la recta BC, entonces M está en el interior del ángulo <BAC
La mediatriz de un segmento en un plano, es el conjunto de todos los puntos del plano que equidistan de los extremos del segmento.
Equidistar
Significa que tienen igual distancia
Toda correspondencia LAA es una congruencia
Toda correspondencia H-C es una congruencia
Figura interactiva 27
Figura interactiva 28
Figura interactiva 29
Figura interactiva 30
Ejercicios
Practica realizando los ejercicios de: la página 167 - 3,4,5,6 ; la página 168 - 14; la página 173 - 6; la página 174 - 9,10,11,12 ; la página 179 - 5,6,7 y demuestra los teoremas 34 y 35
Corolario 4
Ningun triángulo tiene 2 ángulos rectos
Desigualdad en segmentos
Un segmento es menor que otro, si su longitud es menor
Un segmento es mayor que otro, si su longitud es mayor
Desigualdad en ángulos
Un ángulo es menor que otro, si su longitud es menor
Un ángulo es mayor que otro, si su longitud es mayor
Propiedades de las desigualdades
Tricotomía
Transitividad
Aditiva
Multiplicativa
Sean x, y números reales:
1) x < y, ó
2) x > y, ó
3) x = y.
Sean x, y,z números reales:
Si (x < y) y (y < z) entonces:
x<z
Sean a,b,c,d números reales:
Si (a<b) y (c<=d) entonces:
a + c < b+d
Sean a,b,c números reales:
Si (a<b) y (c>0) entonces:
a*c<b*c
Si a= b+c y c>0, entonces a>b
En la página 187, realiza los ejercicios: 6, 7, 8, 9 y 10
Teorema 36
Ángulo externo de un triángulo
Figura interactiva 31
Ángulo internos no contiguos
Teorema 37 - El teorema del ángulo externo
Corolario 5
Teorema 38 - Suma interna de 2 ángulos
En la página 190, realiza el ejercicio 6.
En la página 191, realiza los ejercicios: 9 y 10.
En lapágina 194, realiza los ejercicios: 7, 8 y 9
Ejercicios
Si C está entre A y D, entonces el ángulo <BCD es un ángulo externo del triángulo ABC.
Todo triángulo tiene 6 ángulos externos, y estos forman 3 pares de ángulos opuestos por el vértice
Todo ángulo externo de un triángulo forma un par lineal con uno de los ángulos del mismo triángulo.
El <A y el <B del triángulo ABC se llaman ángulos internos no contiguos de los ángulos externos <BCD y <ACE
El <A y el <C del triángulo ABC se llaman ángulos internos no contiguos de los ángulos externos <CBG y <ABH
El <B y el <C del triángulo ABC se llaman ángulos internos no contiguos de los ángulos externos <BAK y <CAI
Un ángulo externo de un triángulo es mayor que cada uno de sus ángulos internos no contiguos.
Si un triángulo tiene un ángulo recto, entonces los otros ángulos son agudos.
La suma de las medidas de 2 ángulos cualesquiera de un triángulo es menor que 180
Ejercicios
Figura interactiva 32
Teorema 39
Si 2 lados de un triángulo no son congruentes, entonces los ángulos opuestos a estos no son congruentes y el ángulo mayor es opuesto al lado mayor.
Teorema 40 - Reciproco del teorema 39
Si 2 lados de un triángulo no son congruentes, entonces los ángulos opuestos a estos no son congruentes y el lado mayor es opuesto al ángulo mayor.
Ejercicios
En la página 197, realiza los ejercicios 7,8,9,10.
Figura interactiva 33
Teorema 41 - El primer teorema de la mínima distancia
En la página 202, realiza los ejercicios: 3,4,8,9,10
El segmento mas corto que une un punto externo a una recta l y la recta l, es el segmento perpendicular a la recta l.
La suma de las longitudes de dos lados cualquiera de un triángulo es mayor que la longitud del tercer lado.
Ejercicios
Figura interactiva 34
Teorema 42 - La desigualdad del triángulo
Figura interactiva 35
Teorema 43 - Teorema de Charnela
Si 2 dos lados de un triángulo ABC son congruentes respectivamente, con dos lados de un triangulo EDF, y el ángulo comprendido del triángulo ABC es mayor que el ángulo comprendido del triángulo EDF, entonces el tercer lado del triangulo ABC es mayor que el tercer lado del triángulo EDF
Teorema 44 - Reciproco del teorema de Charnela
Ejercicios
En la página 205, realiza los ejercicios 2,3,4,6,7,8,9
En la página 207, realiza el ejercicio 2
En la pagina 209, realiza los ejercicios 8,9,10,12
En la pagina 210, realiza los ejercicios 13,14,15,16,17,18,19,20,270
Si 2 dos lados de un triángulo ABC son congruentes respectivamente, con dos lados de un triangulo EDF, y el tercer lado del triangulo ABC es mayor que el tercer lado del triángulo EDF, entonces el ángulo comprendido del triángulo ABC es mayor que el ángulo comprendido del triángulo EDF
