Capítulo 3: Congruencias, tipos de triángulos y cuadriláteros

Congruencia

En geometría, se dice que dos figuras geométricas son congruentes si tienen la misma forma y tamaño. Las partes coincidentes de las figuras congruentes se llaman homólogas o correspondientes.

Figura interactiva 19

Bisectriz de un ángulo

Teorema 20

Teorema 21 - Adición de ángulos

Teorema 22 - Sustracción de ángulos

Figura interactiva 22

Figura interactiva 23

Mediatriz de un segmento

Figura interactiva 21

Ángulos congruentes

Teorema 15

Teorema 14

Teorema 13

Teorema 12

Teorema 11

Figura interactiva 20

Teorema 16

Teorema 19

Teorema 18 - Teorema de los ángulos opuestos por el vértice

Ángulos opuestos por el vértice

Teorema 17

Congruencia en segmentos

Teorema 23

Teorema 24 - Adición de segmentos

Teorema 25 - Sustración de segmentos

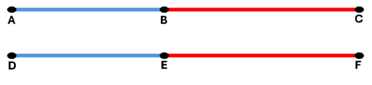
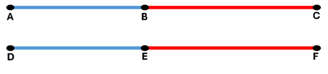
Teorema 26

Congruencia de triángulos

Figura interactiva 24

Lado comprendido

Ángulo comprendido

Figura interactiva 25

Postulado 16 - Postulado LAL

Toda correspondencia LAL es una congruencia.

Postulado 17 - Postulado ALA

Postulado 18 - Postulado LLL

Toda correspondencia ALA es una congruencia.

Toda correspondencia LLL es una congruencia.

Teorema 27- Teorema del triángulo isósceles

Teorema 28 - Reciproco del teorema 27

Si 2 lados de un triángulo son congruentes, entonces los ángulos opuestos a estos lados son congruentes

Corolario 1

Corolario 2

Tipos de triángulos segun sus lados

Tipos de triángulos segun sus ángulos

Si 2 ángulos de un triángulo son congruentes, entonces los lados opuestos a estos lados son congruentes

Triángulo equilátero = 3 lados congruentes

Triángulo isósceles = 2 lados congruentes

Triángulo escaleno = 0 lados congruentes

Triángulo rectángulo = 1 ángulo recto

Triángulo acutángulo = 3 ángulos agudos

Triángulo equiángulo = 3 ángulos congruentes

Triángulo obtusángulo = 1 ángulo obtuso

Todo triángulo equilatero es equiángulo

Todo triángulo equiángulo es equilatero