
Capítulo 1: Puntos, rectas y planos
Definiciones
Corolario
Axioma
Teorema
Afirmación que se acepta sin prueba, porque se considera evidente o fundamental para construir una teoría, y se usan para demostrar otras proposiciones.
Afirmación que se acepta sin demostración. La diferencia entre un axioma y un postulado es que los axiomas son más generales y se aplican a una amplia variedad de áreas matemáticas.
Proposición matemática que ha sido demostrada a partir de axiomas, postulados o teoremas previamente establecidos. La demostración de un teorema es un proceso que sigue reglas lógicas para llegar a una conclusión cierta.
Proposición que se deriva de manera inmediata de un teorema o de una demostración ya establecida, y generalmente se considera como un resultado adicional sin una nueva demostración independiente.
Postulado
Definir conceptos fundamentales como punto, recta y plano en geometría es un desafío porque cada uno depende del otro de manera intrínseca. Por ejemplo, una recta se describe como la unión de una infinidad de puntos alineados en una misma dirección; sin embargo, un punto es conceptualizado como la intersección de dos o más rectas. Y un plano se define como la superficie que resulta de la unión de una cantidad infinita de rectas que se extienden en dos dimensiones, pero, al mismo tiempo, se necesitan puntos para describir las rectas que forman ese plano.


Punto A
Recta
Plano
Punto, recta y plano
Puntos: se sombolizan con letras mayúsculas A, B, C, D, E, ...
Rectas: se simbolizan en términos de dos puntos como o usando las letras l, m, o, p, q, r, s, ...
Plano: se simboliza en términos de tres puntos
Notación
Figura interactiva 2
Figura interactiva 3
Definición de estar entre
Figura interactiva 1
Postulado 5.1
Postulado 5 - Postulado de la recta
Postulado 5.2
Segmento


Rayo
B
C
A
Postulado 4 - Postulado de orden
M
N
P
Postulado 4.1
M
N
Q
Postulado 4.3
Postulado 4.2
M
N
K
Postulado 4.4
M
P
N
X
Postulado 1 - Postulado de la distancia
Postulado 2 - Postulado de la regla
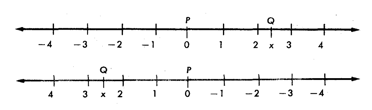
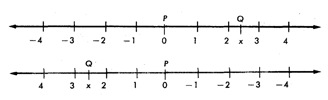
Postulado 3 - Postulado de la colocación de la regla
Rayo opuesto
A
B
C
Hora de prácticar
Ejercicio de demostración
Con lo visto anteriormente, demuestra el siguiente teorema:
Teorema 1
Dada una recta l, existen infinitos puntos que no pertenecen a ella
Teorema 2 - Teorema de localización de puntos
Punto medio
Figura interactiva 4
Teorema 3
Figura interactiva 5
Postulado 6
Figura interactiva 6
Postulado 7 - Postulado del plano
Postulado 6.1
Teorema 4
Alineados o colineales
Coplanarios
Postulado 6


Teorema 5
Figura interactiva 7
Postulado 8
Teorema 6
Figura interactiva 8
Teorema 7
Figura interactiva 9
Teorema 8
Postulado 9
Figura interactiva 10
Conjuntos convexos


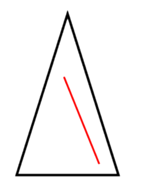

No convexo
Convexo
Figura interactiva 11
Figura interactiva 12
Postulado 10 - Postulado de separación del plano
Postulado 11 - Postulado de separación del espacio
Semiplano
Arista o borde
Semiespacio
Cara
